Week 8 - Support Vector Machines

Exercises

Question 1.

What is the fundemental idea behind "Maximal Margin Classifiers" (as well as their extensions "Support Vector Classifier" and "Support Vector Machines")?

Click here for answer

The fundamental idea behind Maximal Margin Classifiers is to fit the widest possible margin between the classes. In other words, the goal is to have the largest possible "street" between the decision boundary that separates the two classes and the training instances.

Question 2.

What is a support vector?

Click here for answer

After training an SVM, a support vector is any instance located on the margin (see the previous answer), or between them when using soft margins (see later question). The decision boundary is entirely determined by the support vectors. Any instance that is not a support vector has no influence on the decision boundary. Computing the predictions only involves the support vectors, not the whole training set.

Question 3.

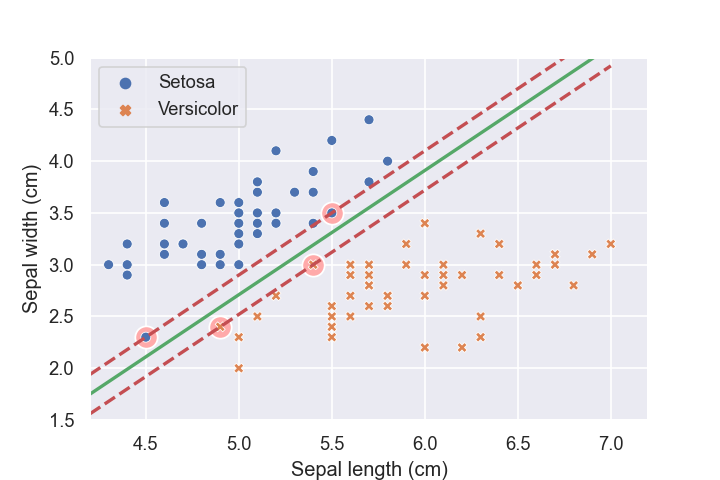
In the plot below, which points are the "support vectors"?

Click here for answer

It uses more than 1 here for each class, although which ones are quite tricky to discern. Don't worry if you got a few of the points wrong here, the main thing is to note that sometimes it can be more than one point per class!

Question 4.

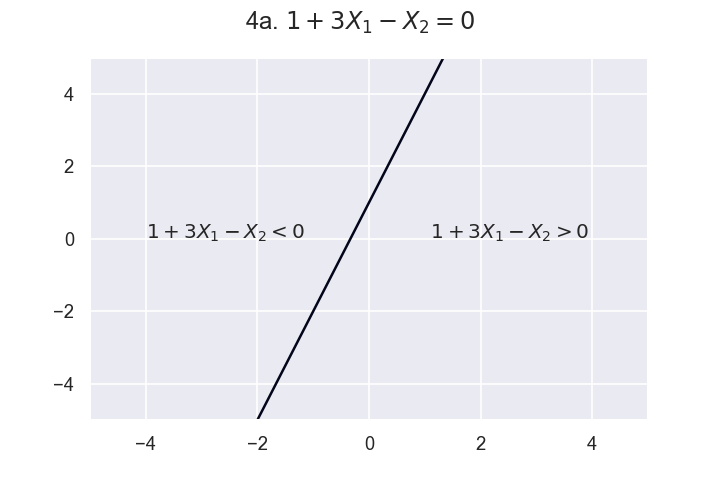
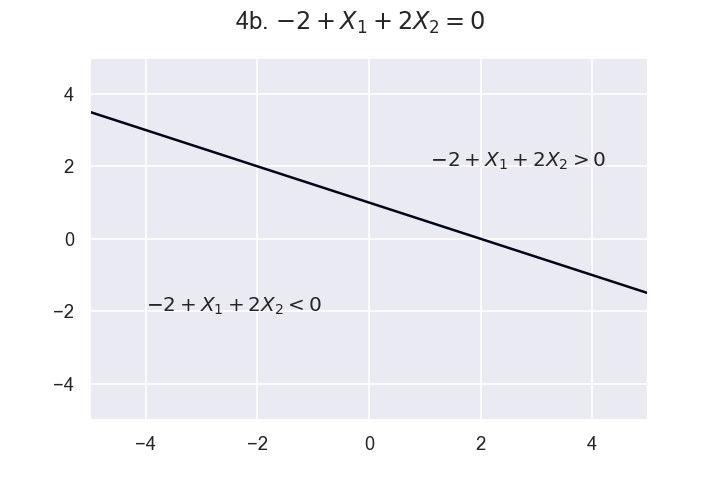
Sketch or code (using Python) the following two dimensional hyperplanes, indicating where $1 + 3X_1 - X_2 > 0$ and where $1 + 3X_1 - X_2 < 0$.

a. $1 + 3X_1 - X_2 = 0$

Click here for answer

b. $-2 + X_1 + 2X_2 = 0$

Click here for answer

Question 5.

Fundamentally, how are "Support Vector Classifier" and "Support Vector Machines" extensions of "Maximal Margin Classifiers"?

Click here for answer

When using a Support Vector Classifier (or soft margin classification), the SVC searches for a compromise between perfectly separating the two classes and having the widest possible street (i.e., a few instances may end up on the street).

Support Vector Machines use kernels when training on nonlinear datasets.

Question 6.

If $C$ is large for a support vector classifier in Scikit-Learn, will there be more or less support vectors than if $C$ is small? Explain your answer.

Click here for answer

When the tuning parameter $C$ is large in Scikit-Learn, then there are less support vectors, meaning fewer observations are involved in determining the hyperplane. The strength of the regularization is inversely proportional to $C$, meaning a large $C$ has a higher penelty.

Question 7.

Is the "confidence score" output from a SVM classifier the same as a "probability score"?

Click here for answer

No, the output of the SVM, the distance between the test instance and the decision boundary, cannot be directly converted into an estimation of the class probability.

Note If you set probability=True when creating an SVM in Scikit-Learn, then after training it will calibrate the probabilities using Logistic Regression on the SVM’s scores (trained by an additional five-fold cross-validation on the training data). This will add the predict_proba() and predict_log_proba() methods to the SVM.

Question 8.

Say you trained an SVM classifier with an RBF kernel. It seems to underfit the training set: should you increase or decrease $\gamma$ (gamma) and/or $C$?

Click here for answer

If an SVM classifier trained with an RBF kernel underfits the training set, there might be too much regularization. To decrease it, you need to increase gamma or C (or both).

[NbConvertApp] Converting notebook SVM_Exercises.ipynb to html
[NbConvertApp] Writing 277380 bytes to SVM_Exercises.html